Algebra is one of the hardest systems of math we learn in school. But what makes it so hard is also what makes it so important.
You can almost think of Algebra like our first real language of math. It is full of complex rules that layer on top of one another, building up to something that is much more than the sum of its parts. Without language, our ability to communicate would be very limited. Without Algebra, our mathematical thought would be similarly limited.
If things are going well, you might start to notice your brain working differently. You start “thinking in Algebra”, instead of just “translating”. But if things aren’t going well, you just get the sense that things aren’t adding up.
Essentially, Algebra is so hard because it requires us to completely change the way we think. But once we achieve some fluency, it starts to open up a whole new world of thought. Read on to learn about Algebra, the key concepts that make up Algebra, how to make Algebra feel easier, and more.
What Even is Algebra, Really?
Before we can demystify Algebra and make it more accessible, we have to know what we’re even talking about.
Essentially, Algebra is a system for defining and exploring relationships between variables. Variables can represent almost anything: time, distance, energy, flow rate, happiness, hunger!
A simple relationship might be between how hungry you are and the time since your last meal. A complex relationship might be between a stream’s flow rate and local precipitation, watershed area, soil characteristics, vegetation type, etc.
Algebra unlocks our ability to define and explore these relationships. This provides the mathematical foundation upon which we break down and understand the complexity of the world.
It’s kind of a big deal!
Grasping The 3 Big Ideas of Algebra
It’s easy to get lost in all the minutiae whenever learning something new. Algebra contains so many unique concepts, each with their own underlying rules, and all of these concepts and rules interact with each other. This can feel overwhelming in its complexity.
But all of these rules and concepts trace back to 3 big ideas:
- Algebraic Properties
- Variable Relations
- The Cartesian Plane
If you try to think about how each rule you learn feeds into one of these big ideas, you’ll float above the minutiae and develop more of an intuitive understanding. But of course, first you need to know what these 3 big ideas are.
Algebraic Properties
We’re going to start with the basics. In Algebra, there are five foundational properties that underlie basically everything else. If you’ve taken Pre-Algebra hopefully some of these seem familiar.
- Identity Property
- Commutative Property
- Associative Property
- Distributive Property
- Inverse Property
Often these are taught to students without much fanfare and with an outsized emphasis on memorizing the property names. But the substance of these properties is what really matters, and the more you can internalize them the better. In other words, you want to know them so well that you don’t even realize you know them. You want them to become obvious.
Let’s jump in!
Identity Property
The Identity Property states that any number can be multiplied by 1 or added to zero without effect.
For example:
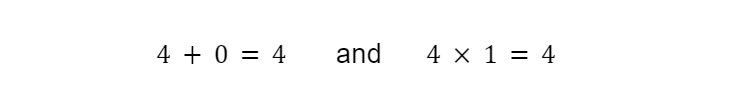
If you’re well into Algebra, this property may not seem like big exciting news. It may already seem obvious. But we build on the identity property in many different ways, some of which might not be as obvious.
For example, how do I know the following is true?

One way of thinking about this is by applying the identity property.
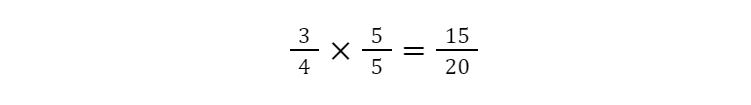
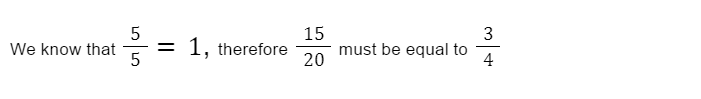
Commutative Property
The Commutative Property states that for multiplication and addition, you can change the order of the numbers without changing the result.
For example:
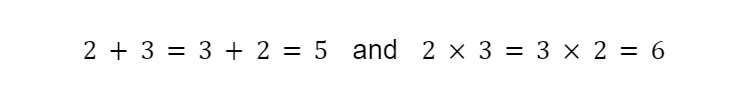
This doesn’t apply for division and subtraction.
For example:
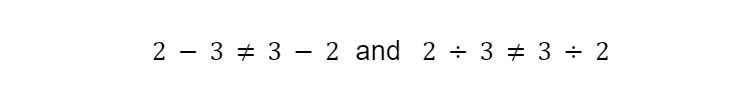
In Algebra, we like to move things around, manipulating equations and inequalities to isolate variables or quantities. With that in mind, it can be helpful to reframe subtraction as addition-of-a-negative-number. That way the commutative property applies.
For example:
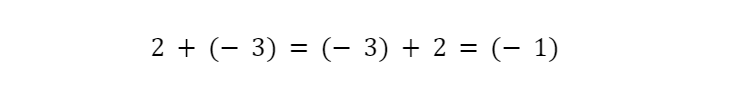
We can do the same sort of reframing with division as multiplication-by-a -fraction.
For example:
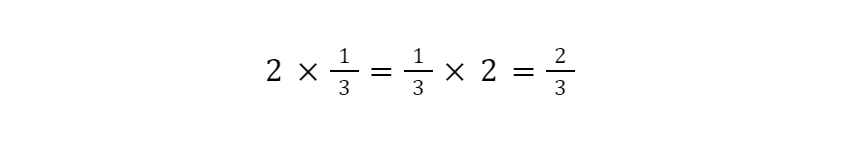
Associative Property
The associative property states that for multiplication and addition, you can change the grouping of the numbers without changing the result.
For example:
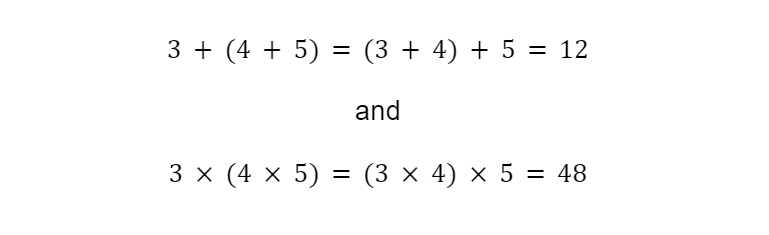
This doesn’t apply for division and subtraction.
For example:
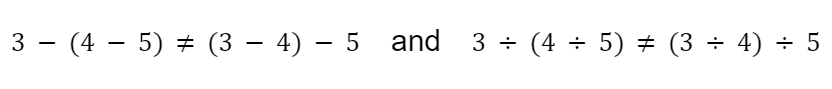
If we follow order-of-operations (a.k.a PEMDAS), we know to perform the operations inside the parentheses first. But the associative property tells us when the parentheses don’t really matter. This is useful in Algebra because we are often dealing with unknown quantities (a.k.a variables) that can’t be readily operated on.
Let’s say I had…
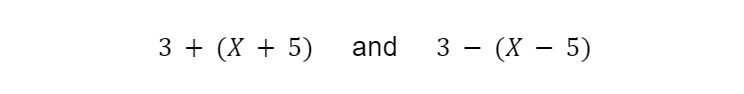
For the first expression, I know the grouping doesn’t matter, so I can just drop the parentheses and combine like terms…
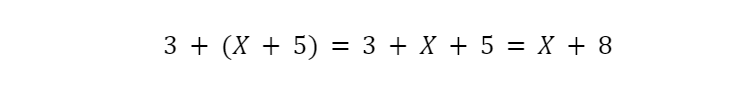
For the second expression, I know the grouping does matter. Because I can’t actually combine (X-5) I’m stuck.
At least until we get to our next Algebraic property…
Distributive Property
The Distributive property states that a multiplication between two groups can be resolved by multiplying every term in one group by every term in the other.
For example:
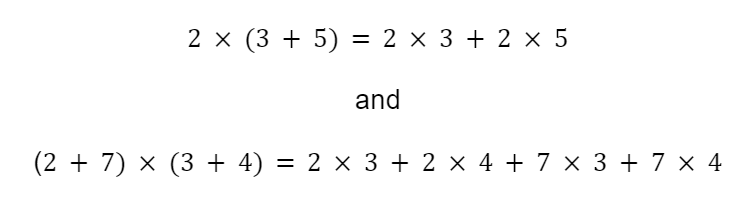
Check out our post on area models for a better way to visualize distribution between large groups.
Let’s look at the last expression from the associative property example:
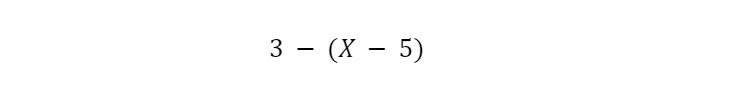
At first glance it might not seem like the Distributive property applies. Where is the multiplication?
But we can use another algebraic property, the Identity property, to help us out. Let’s rewrite it as…
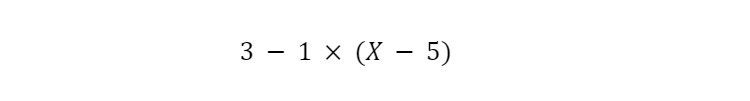
Now we can distribute the (-1) and simplify…

Inverse Property
Last but not least we have the Inverse Property. It states that when we subtract a number from itself, we get zero, and when we divide a number by itself, we get one.
For example:
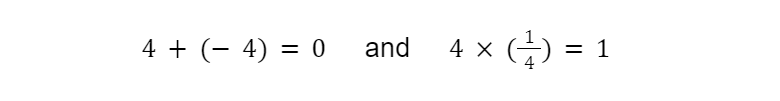
In Algebra, we take the inverse property to great heights, applying it not only with numbers but with complex variable expressions.
For example, using the inverse property of multiplication followed by the identity property of multiplication, we can simplify the following variable expression:
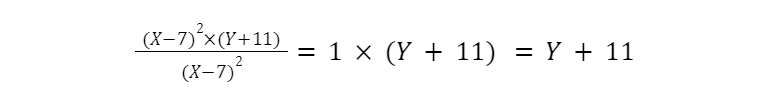
How To Build Up From Here
Often, when we learn a new rule or concept, we look at it like it is on an island, untethered from every other rule that we’ve learned. But the reality is that most of the “new” concepts you learn are just different applications of the properties above.
Once you build up one layer of complexity on top of these properties, you build up another layer, and then another. As you advance it may start to feel like what you’re doing has nothing to do with the Commutative Property. But chances are, it does!
You’ll notice that I sometimes used more than one algebraic property as I explored different examples. As you practice your Algebra, try to think about what properties are at play. If you feel stuck in a particular problem, try to think about what properties might apply.

Variable Relations
Once we have our Algebraic properties down, we introduce the real star of the show, variable relations. Variable relations are how we apply algebra to the real world. They allow us to ask big questions and then come up with the answers. But before we can do any of that, we have to first rework our understanding of what an equation is.
Redefining What An Equation Is
Prior to learning algebra, an equation has a left-to-right sense of direction. Take something like…
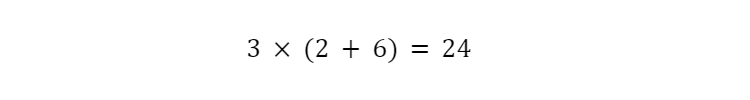
On the left side, we perform a series of operations. On the right side we get our solution. On a test, maybe the problem looks like this…
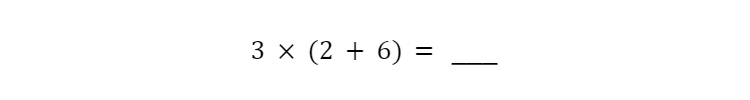
We do the math and voila, we get 24.
In Algebra, this exact same equation might be presented a bit differently…
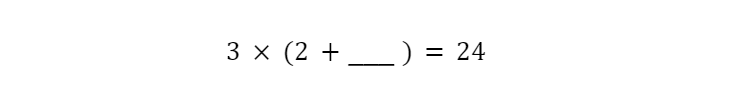
The difference here is where we’ve placed our “unknown.” Instead of it being the “result” of our equation, it is mixed up inside the expression on the left. It seems like a small change, but it forces us to consider the equation in a different way.
Now, the equation doesn’t just flow left-to-right. Instead, there is a left side and a right side that we know must be equal to each other (hence the equal sign). Our goal is not to perform some operations and get a result. Our goal is to define the unknown such that our equation is true.
Stay with me!
In the above equation, there is only one value that makes sense. But what if we set it up with two unknowns instead of just one?
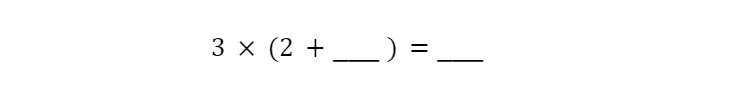
At this point, we have a need for a new type of symbol to help represent our unknowns. This is where variables like X and Y come into play. We let X represent the first unknown and let Y represent the second.
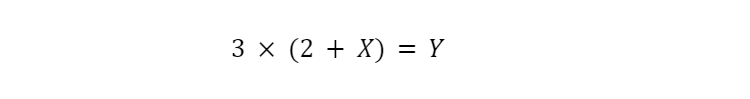
We already know one way to make this equation true, X=6 and Y=24. But that is now just one of infinitely many solutions. It could also be that X=1 and Y=9. Or X=100 and Y=306
Essentially what we have now is a relationship between two variables, X and Y. As X changes, so does Y, and vice versa.
The Big Picture of Variable Relations
The equation I’m using here is just a contrived example, and the variables don’t represent anything in particular. Using simple, contrived, and meaningless equations allows us to focus on whatever particular algebraic rule we might be trying to explore. But it also takes us away from the big idea at the heart of all our learning. With that in mind, let’s zoom back out.
Because variables can represent basically any quantity, we can create equations (or inequalities) to model relationships of all kinds. With these variable relations, we can start to ask more complicated questions about the world around us. How do populations grow over time? How does rolling down the window affect my car’s gas mileage compared with turning on the A.C.?
Of course, we need more information to help us define these relations, but Algebra provides the framework we need to set them up and explore their depths.
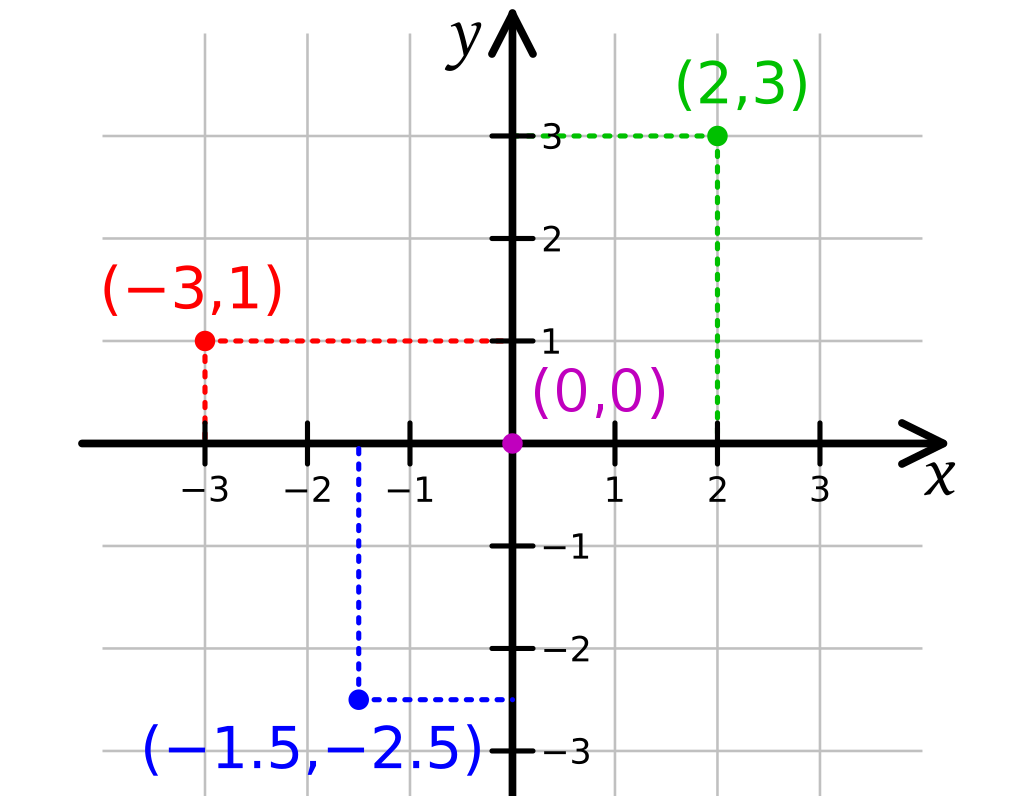
The Cartesian Plane
Lastly, the Cartesian plane is what we typically use to graph variable relations (among other things). It’s defined by two perpendicular axes (typically X and Y), intersecting at an origin (where X = Y = 0). Math speak aside, this is the big idea of Algebra that likely feels the most familiar.
We tend to understand visuals better than hard numbers, so fancy graphs and charts are how complex information about the world is often presented to us. The coordinate system of choice is the Cartesian plane.
But why?
Believe it or not, the Cartesian plane is not the only 2 dimensional coordinate system out there, (see polar coordinates). There are other ways to visualize variable relations, each with different advantages and disadvantages. But they are all equally abstract and arbitrary.
With that in mind, the fact that most of us can readily understand graphs when they are presented to us is a testament to our ability to internalize abstract mathematical ideas. We “think” in Cartesian coordinates, not because that is inherent, but because we learned it.
How To Make Algebra Feel Easier
Big ideas take time to settle in. And just like with learning a language, you may not feel like you’re making progress in Algebra until you’ve had a chance to develop some fluency. It takes perseverance.
But really, the secret to making Algebra feel easier is all about developing a growth mindset. There is a split that happens when students hit middle school and start learning Algebra. Up to that point, most students have an appreciation and interest in math. Or at the very least they feel neutral.
But learning Algebra can make math feel too abstract, obtuse, pointless, etc. to the point where students become disinterested and disengaged. Even worse, they start to feel negatively about their own abilities, saying things like, “I’m not a math person” or “I’m bad at math.”
If you go into a learning experience predisposed towards failure, you are likely going to fall short of your true potential. But, if you go into a learning experience with a positive mindset, you might surprise yourself with what you can achieve.
Emergent Education is a K-12 tutoring company based in Portland, OR. We offer in-person tutoring locally and online tutoring to students across the U.S.
If you’re interested in leveling up your Algebra skills, check out our math tutoring services.
